Mathematics 02
Aperçu des sections
-
-
-
-
This space is for audiovisual communication between the professor and the students
-
-
Mathematics 2 cours is one of the systematic teaching units of the composition offerings in the LMD system, taught in the second semester of the first year of the Bachelor of Common Core, Mathematics is a set of abstract knowledge resulting from logical conclusions applied to groups. quantitative topics, helping us to understand, compare and understand the world around us and develop the ability to think properly and reasonably, Mathematics is involved in many other fields such as technology and science, helping researchers and scholars find solutions to problems and make the right decisions.
Mathematics helps provide logical solutions and address everyday issues such as project planning, project management, budgets and even discussion management.
-
Contact info:
Professor: Benfreiha Nadjet
University: Djilali bounaama University, Khamis Milaina
Faculty: of Economic and Commercial Sciences and Management Sciences
Department: of Commercial Sciences
Professional Email: nadjet.benfreiha@univ-dbkm.dz
All your concerns about the lecture or business addressed via professional email are answered within 48 hours.
-
Syllabus Teaching Material Handbook
Djilali bounaama – khemis meliana-
university
Faculty of Economic, Commercial and Management Sciences
Faculty
Common core
section
first year
level
Benfreiha Nadjet
Teacher
Mathematics 2
course name
Methodology
Teaching Unit
Lecture + oriented works
Lesson type
Second
semester
02
coefficient
04
credit
3 hours
number of hours per week
14 weeks in the first semester about 42 hours
Courier Size
an hour and a half
Lecture
an hour and a half
directed works
All your concerns about the lecture or business addressed via professional email will be answered within 48 hours.
nadjet.benfreiha@univ-dbkm.dz
e-mail
Method of Communication
-
At the end of this course, the student will be able to:
• Empowered in the areas of research, interpretation, and the ability to make sound decisions.
• Identify quantitative methods used in data processing, linear functions, and dealing with matrices.
• Gain a clear vision of the most important aspects of mathematics, which will enable him to work in different fields of life, such as economics and trade.
• Deal with methods of thinking and form and develop sound mathematical trends.
• Accurate and correct understanding of the most important topics of mathematics 02.
• Provide a range of experiences in the field of mathematics to help him present the results of qualitative economic research in a specific, clear, concise and accurate quantitative manner.
.
-
To support the cours and be able to understand it well, it is necessary to have the following knowledge:
the concept of functions and derivatives, as well as integrals and basic methods for numbers, in addition to a good knowledge of the mathematical aspects. Also, a good understanding of the quantitative, arithmetic and mathematical methods prior to this cours.
-
-
Dear student, if you are unable to answer the pre-learning questions, I ask you to review the file included to enhance your knowledge about Mathematics 02.
-
-
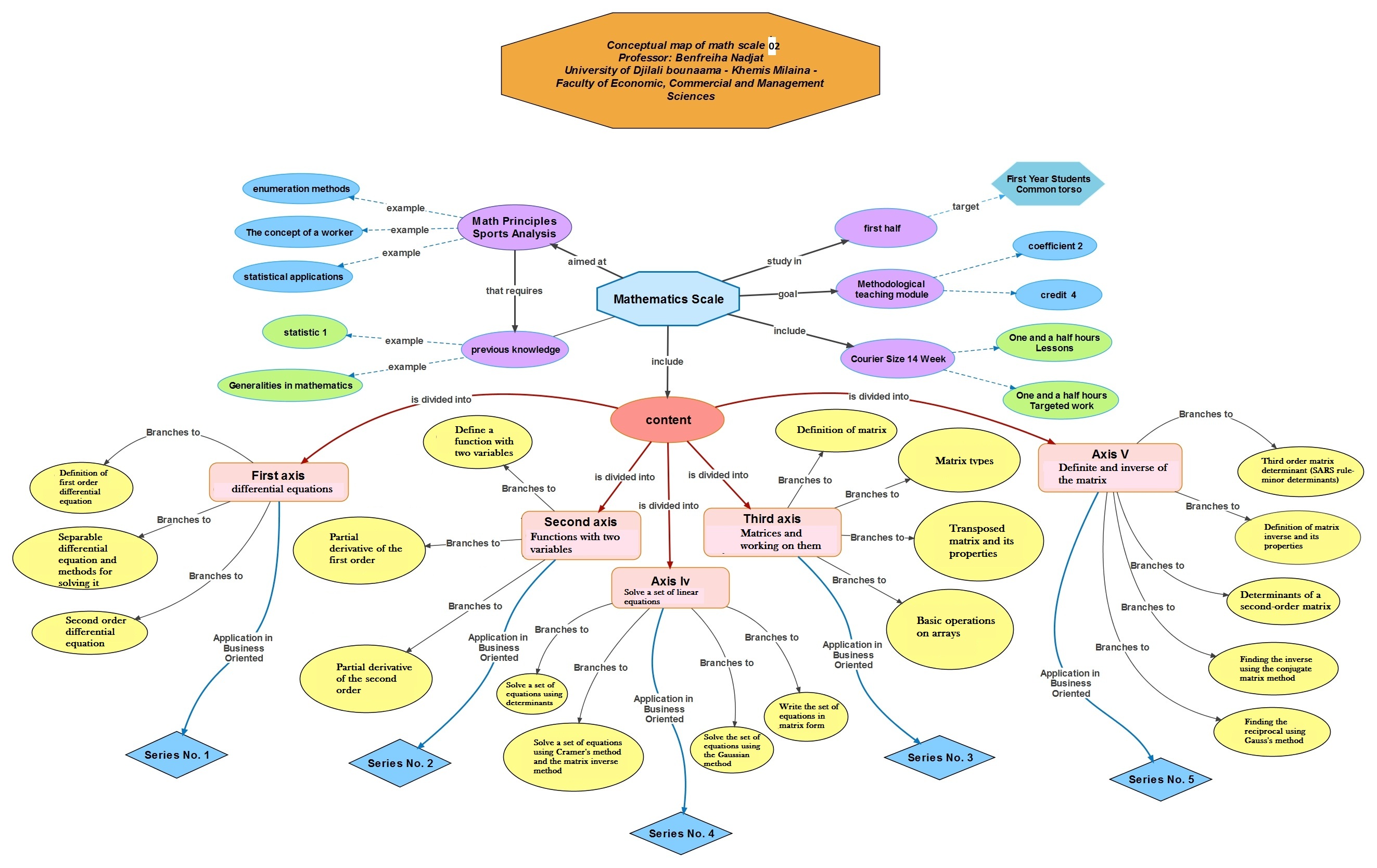
The following map is a detailed course plan
-
Dear student, to view a detailed mathematics lesson plan click on the URL upon.
-
-
Introduction:
Mathematics is a study mainly related to representation and reasoning about abstract objects such as numbers and spaces. It is mainly used in many fields such as natural sciences, engineering, medicine, and several other fields. It also works to develop new specializations in the field of mathematics, such as statistics, and thus there is no dividing line between theoretical and applied mathematics.
Mathematics Standard 02 is directed to first-year bachelor’s students. It has been divided into five axes, including 16 lessons divided over 14 weeks. The first axis includes differential equations of the first order and second order, and it is a continuation of the fifth axis: Integrals, which is the last axis in Mathematics 01 for the hexagram. the first.
The second axis includes functions with two variables by presenting general concepts and then addressing partial derivation of the first and second order.
As for the third axis, it included matrices and working on them, where we will provide a definition of the matrix, its types, and the most important operations on it.
In the fourth axis, we will discuss the determinants and inverses of the matrix, of the second and third order, and we will present the properties of determinants, and finding the inverses of the matrix in several ways.
Through the fifth axis, we will learn about solving a set of linear equations, by writing the sentence in matrix form and solving it in several ways.
-
By the end of this axis the student will be able to:
1. Level of knowledge and remembrance: Students at this level recover information from memory (tribal gains), where students save definitions associated with the subject of mathematics, acquire the necessary skills that enable them to use optimal methods of counting and the student is given multiple choice questions, and is asked to answer them.
2. Level of assimilation and understanding: The student clarifies the basic characteristics that allow him to review the various theories and concepts in the axis. Here, the student gives some varied questions based on what has been used and understood for the study.
3. Students learn about various concepts related to differential equations, and use this to quantify and interpret different economic phenomena, and ask students to clarify the concepts by providing relevant examples of reality and working life.
4. Level of Analysis: Students distinguish between field working methods, having the student study the most important methods of dissemination.
5. Students investigate the role of differential equations in various economic activities through careful examination, and here students brainstorm to find the causes of the problem and how to solve it from the benefits of the lectures provided.
6. The student studies the concepts of first- and second-order differential equations, based on the resources and tools available to them and measure them. We develop a final exercise in which the various processes around the axis are determined.
-
-
-
Dear student, try to solve the solve exercises.If you cannot you have to re-read the lesson and apply examples.
-
Dear student, you can see the following solution to evaluate your understanding of the lesson.
-
Dear student, you can use the following explanatory clip to support your information.
-
-
-
-
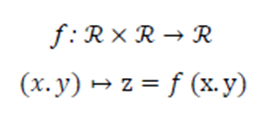
At the end of this axis, the student will be familiar with the objectives of the axis based on Bloom’s levels of knowledge:
1. Knowledge and memory level: Students at this level retrieve and organize information from memory (a priori acquisitions), where students become familiar with the concept of functions with two variables, and provide them with the necessary skills that enable them to use optimal methods to calculate partial derivatives of the first and second order, and the student is given Multiple choice questions, and he is asked to answer them. They can also be given fill-in-the-blank questions, the goal of which is to restore his tribal gains related to the axis.
2. The level of comprehension and understanding: The student identifies and identifies the various variables and concepts related to the second axis. Here we give the student some various questions based on what was learned and evaluated for the lesson.
3. Application level: The student is able to perform operations to identify functions with two variables and apply them
4. Level of analysis: The student distinguishes various calculation methods related to countries with two variables.
5. Structure level: Students organize information in different ways through brainstorming.
6. Evaluation level: The student evaluates and evaluates all the information acquired so that decisions are made based on the specified criteria. We develop a final exercise in which he determines the various operations of functions with two variables.
-
-
Dear student, try to solve the solve exercises.If you cannot you have to re-read the lesson and apply examples.
-
Dear student, you can see the following solution to evaluate your understanding of the lesson.
-
Dear student
Here are some questions about the second axis of Mathematics Scale 02
-
-
Dear student, you can use the following explanatory clip to support your information
-
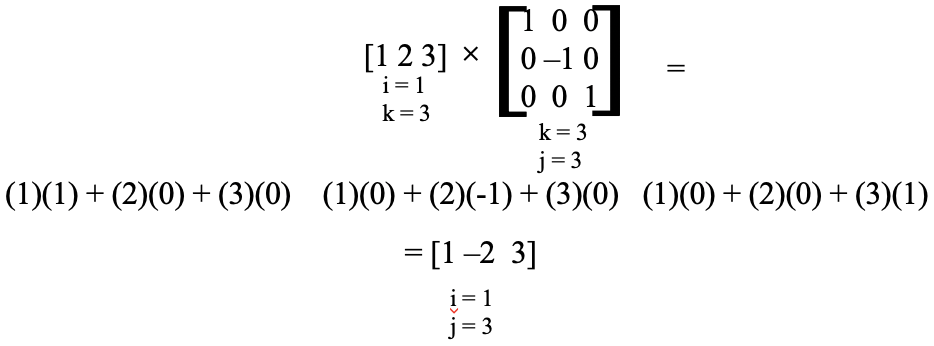
At the end of this axis the student will be able to:
1. Knowledge and memory level: Students at this level retrieve and organize information from memory (prior acquisitions), where students learn about the concept of matrices and their types, and provide them with the necessary skills that enable them to perform basic operations on them. The student is given multiple choice questions, and is asked to answer them. They can also give them fill-in-the-blank questions, aimed at restoring their tribal gains related to the axis.
2. The level of comprehension and understanding: The student identifies and identifies the various variables and concepts related to the third axis. Here we give the student some various questions based on what was learned and evaluated for the lesson.
3. Application level: The student can perform operations to learn about applications about matrices and operations on them.
4. Analysis level: The student distinguishes the various types of matrices as well as their basic operations.
5. Structure level: Students organize information in different ways through brainstorming.
6. Evaluation level: The student evaluates and evaluates all the acquired information in order to make decisions based on the specified criteria. We develop a final exercise in which he identifies the various matrix operations.
-
-
Dear student, try to solve the exercises. If you cannot you have to re-read the lesson and apply examples
-
Dear student, you can see the following solution to evaluate your understanding of the lesson.
-
-
Dear student, you can use the following explanatory clip to support your information
-
By the end of this axis, the student will be able to:
1. Knowledge and memory level: Students at this level retrieve and organize information from memory (prior acquisitions), where students learn about the determinants and inverses of a matrix, and provide them with the necessary skills that enable them to find the inverses of a matrix. The student is given multiple choice questions, and is asked to answer them. They can also be given fill-in-the-blank questions, the goal of which is to restore his tribal gains related to the axis.
2. The level of comprehension and comprehension: The student identifies and identifies the various variables and concepts related to the fourth axis. Here we give the student some various questions based on what was learned and evaluated for the lesson.
3. Application level: The student is able to perform operations on the determinants and inverses of matrices and learn about various methods for doing so.
4. Level of analysis: The student distinguishes the various operations related to the axis.
5. Structure level: Students organize information in different ways through brainstorming.
6. Evaluation level: The student evaluates and evaluates all the information acquired so that decisions are made based on the specified criteria. We develop a final exercise in which he identifies the various operations of determinants and inverses of the matrix.
-
-
Dear student, try to solve the exercises. If you cannot you have to re-read the lesson and apply examples
-
Dear student, you can see the following solution to evaluate your understanding of the lesson.
-
Dear student
Here are some questions about the fourth axis of Mathematics Scale 02
-
-
Dear student, you can use the following explanatory clip to support your information
-
By the end of this axis the student will be ablre to:
1. Knowledge and memory level: Students at this level retrieve and organize information from memory (prior acquisitions), where students learn basic concepts about writing a set of equations in matrix form, and provide them with the necessary skills that enable them to solve a set of linear equations in several ways, and are given The student is given multiple choice questions, and is asked to answer them. They can also be given fill-in-the-blank questions, the goal of which is to restore his prior gains related to the axis.
2. The level of comprehension and comprehension: The student identifies and identifies the various variables and concepts related to the fifth axis. Here we give the student some various questions based on what was learned and evaluated for the lesson.
3. Application level: The student is able to perform operations on sets of linear equations and solve them with methods such as Gauss, Cramer, or determinants....
4. Analysis level: The student distinguishes various operations on solutions to sentences of linear equations.
5. Structure level: Students organize information in different ways through brainstorming.
6. Evaluation level: The student evaluates and evaluates all the information acquired in order to make decisions based on the specified criteria. We develop a final exercise in which he identifies the various processes for solving a set of linear equations.
-
-
Dear student, try to solve the exercises. If you cannot you have to re-read the lesson and apply examples.
-
Dear student, you can see the following solution to evaluate your understanding of the lesson
-
-
Dear student, you can use the following explanatory clip to support your information
-
Complete the final evaluation on time
Important Note: The time limit for completion of the final evaluation is 60 minutes and two attempts
If you fail in the exam, you must review your lessons
-
-
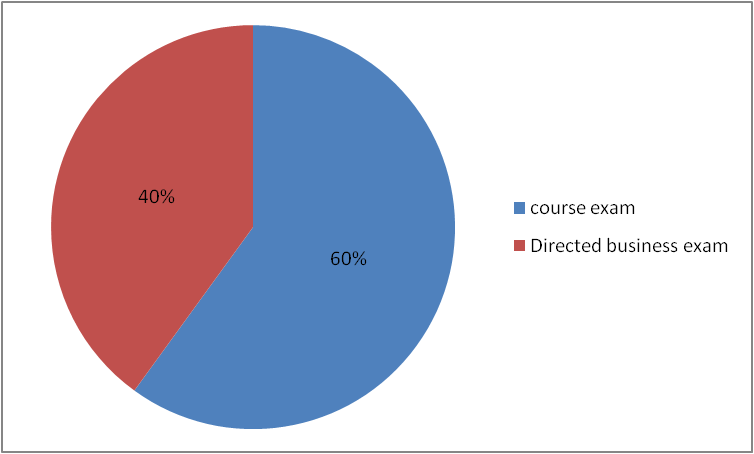
To pass this subject, you must obtain a grade greater than or equal to 10 out of 20. If this is not possible, you can take the remedial course exam, where the course grade is calculated through the regular course exam, which represents 60%, and the directed work point, which represents 40%.
-
he student must see all the references at his disposal in order to ensure the good way to acquire all the targeted competencies and thus the proven success. Among the references we place in the students' hands are the following:
Mas' adan Hadi and Hanashi Farah, General Mathematics of Economists, edition 1, Noran Publishing and Distribution, Tibsa, Algeria, 2021.
· Hussein Yassin Tamah, Mathematics for Economics, Administrative and Financial Sciences, T1, Dar Al Safa for Publishing and Distribution, Amman, Jordan, 2010
· .Jacques Dixmier (2001), Cours de mathématiques du premier cycle 1re année– Avec exercices corrigès, Deuxième édition, Dunod, Paris, France.
4. Jacques Vélu (2020), Mathématiques Générales - Cours et exercices corrigès, Dunod, Paris, France.
-
My wishes to dear students for success, thank you.
