Information quantique

Topic outline

• Select topic General

  General

  Collapse all Expand all

  L'information quantique est la théorie de l'utilisation de spécificités de la physique quantique pour le traitement et la transmission de l'information.

  • Select activity Announcements

    

    Announcements Forum

    Introduire l'information quantique et l'informatique quantique.
    Prérequis recommandés Cours de mécanique quantique I et II du programme de licence de physique.

• Select topic Fiche de contact

  Fiche de contact

  Université : Djilali Bounaama Khemis Miliana

  Faculté: Science de la matière et d'informatique

  Département : Physique

  Spécialité : Physique théorique

  Niveau : Master 2 Physique théorique

  Matière : Informatique quantique

  Semestre : 03

  Coefficient : 03

  Crédits : 06

  Conférencier : Dr Hocine Boukabcha.

  Contact : Vous pouvez me contacter sur h.boukabcha@univ-dbkm.dz
• Select topic Objectifs

  Objectifs
  1. Synergie de collaboration : Renforcer la collaboration transdisciplinaire entre chercheurs de différentes institutions pour encourager des projets communs.
  2. Échanges internationaux : Favoriser les interactions avec des chercheurs d'autres pays par l'organisation d'événements et de visites.
  3. Formation spécialisée : Améliorer la formation d'étudiants et de personnel qualifié en les intégrant dans un environnement interdisciplinaire.
  4. Partage d'infrastructures : Promouvoir la découverte scientifique grâce à une gestion efficace des infrastructures de recherche.
  5. Développement technologique : Initier des innovations technologiques et faciliter l'interaction avec l'industrie pour le transfert de technologies.
• Select topic PRE-REQUIS

  PRE-REQUIS

  Pour étudier l'information quantique, plusieurs prérequis sont nécessaires, tant sur le plan théorique que pratique. Voici un aperçu des compétences et connaissances requises :

  Compétences Mathématiques

  1. Algèbre Linéaire : Une compréhension solide de l'algèbre linéaire est essentielle, car elle est utilisée pour manipuler les états quantiques représentés par des vecteurs dans des espaces de Hilbert. Les cours recommandés incluent :
     • MAT165 : Algèbre linéaire et analyse vectorielle
     • MAT472 : Algèbre linéaire et géométrie de l’espace.
  2. Probabilités et Statistiques : La capacité à comprendre et à manipuler les concepts de probabilités est cruciale, car les mesures en mécanique quantique sont intrinsèquement probabilistes. Un cours de probabilités comme STT290 est souvent requis.
  3. Mathématiques Discrètes : La maîtrise des mathématiques discrètes est également importante pour la compréhension des algorithmes et des structures de données utilisés en informatique quantique.

  Connaissances en Physique

  1. Mécanique Quantique : Une connaissance de base des principes de la mécanique quantique, y compris la superposition et l'intrication, est fondamentale pour comprendre comment l'information quantique diffère de l'information classique.
  2. Systèmes Quantique : Comprendre les systèmes quantiques et leurs comportements est essentiel pour modéliser et analyser des phénomènes quantiques.

  Compétences en Informatique

  1. Programmation et Algorithmie : La maîtrise de la programmation classique ainsi que des algorithmes quantiques est nécessaire. Cela inclut la compréhension d'algorithmes comme ceux de Grover et Shor, qui exploitent les propriétés quantiques pour résoudre des problèmes spécifiques plus efficacement que les algorithmes classiques.
  2. Structures de Données : La connaissance des structures de données est importante pour l'implémentation d'algorithmes quantiques et leur optimisation.
• Select topic Table des matières

  Table des matières

  1 Qu'est-ce qu'un qu-bit ?
                1.1 Polarisation de la lumière
                1.2 Polarisation d'un photon .
                1.3 Formulation mathématique : le qu-bit
                1.4 Principes de la mécanique quantique
                1.5 Générateur quantique de nombres aléatoires
                1.6 Cryptographie quantique
  2 Manipulations d'un qu-bit
                2.1 Sphère de Bloch, spin 1/2
                2.2 Évolution dynamique
                2.3 Manipulations de qu-bits : oscillations de Rabi
  3 Corrélations quantiques
                3.1 états à deux qu-bits
                3.2 Opérateur densité et entropies
                3.3 Théorème de non clonage quantique
               3.4 Inégalités de Bell
               3.5 Téléportation
  4 Introduction au calcul quantique
               4.1 Calcul réversible
               4.2 Portes logiques quantiques
               4.3 Transformation de Fourier quantique
               4.4 Période d'une fonction
               4.5 Réalisations physiques
• Select topic Chapitre 01 : Q'est ce que un qubit?

  Chapitre 01 : Q'est ce que un qubit?

  Qubit ou bit quantique

  Espace de Hilbert

  Polarisation d'un photon

  Qubits et postulats quantiques

  

  • Select activity CHapitre_01

    

    CHapitre_01 File
  • Select activity Serie_01

    

    Serie_01 File
• Select topic Chapitre 02 : Manipulations d'un qu-bit

  Chapitre 02 : Manipulations d'un qu-bit

  

  Sphère de Bloch et Spin 1/2

  La sphère de Bloch est un outil graphique essentiel en mécanique quantique pour représenter les états de spin d'une particule de spin 1/2, souvent appelée qubit. Cette représentation permet de visualiser les états quantiques dans un espace tridimensionnel, facilitant ainsi la compréhension des transformations et des mesures associées à ces états.

  Concepts Fondamentaux

  1. Spin 1/2:
     • Un système de spin 1/2, comme un électron, a deux états fondamentaux, généralement notés ∣+⟩ et ∣−⟩ le long d'un axe (souvent l'axe z). Ces états sont orthogonaux et peuvent être représentés par des vecteurs dans un espace complexe de dimension deux.
     • Tout état de spin peut être exprimé comme une superposition de ces deux états:                   ∣ψ⟩=a∣+⟩+b∣−⟩
       où a et b sont des coefficients complexes satisfaisant la condition de normalisation               ∣a∣² +∣b∣²=1.
  2. Sphère de Bloch:
     • La sphère de Bloch est un modèle géométrique qui représente tous les états possibles d'un qubit sur la surface d'une sphère. Chaque point sur cette sphère correspond à un état quantique unique.
     • Les coordonnées sur la sphère sont souvent données par deux angles, θ et ϕ, qui définissent la position d'un point sur la sphère:
       • L'angle θ varie de 0 à π (pôle nord à pôle sud).
       • L'angle ϕ varie de 0 à 2π (autour de l'axe vertical).

  Représentation Mathématique

  La relation entre les coordonnées sphériques et l'état du qubit est donnée par:

  ∣ψ⟩=cos⁡(θ2) ∣+⟩+e^iϕ sin⁡(θ2) ∣−⟩

   

  Cela montre comment chaque point sur la sphère peut être associé à un état quantique.

  

   

  • Select activity Introduction à l'information quantique

    

    Introduction à l'information quantique URL
• Select topic Chapitre 03 : Corrélation quantiques

  Chapitre 03 : Corrélation quantiques

  Produit tensoriel et états intriquées

  Théorème de Bell et interférences des états corrélés.

  • Select activity Corrélation quantiques

    

    Corrélation quantiques File
• Select topic Chapitre 04 : Calcul quantique

  Chapitre 04 : Calcul quantique

  Notion de calculateur

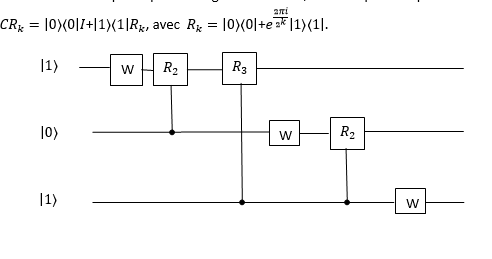
  Les circuits quantiques

  Parallélisme quantique

  Portes de contrôle et génération d'intrication

  Portes quantiques universelles

  

  • Select activity Calcul quantique

    

    Calcul quantique File
  • Select activity Serie_02

    

    Serie_02 File
• Select topic Devoir

  Devoir
  • Select activity Devoir

    

    Devoir File
• Select topic Références

  Références

  1-      1- Michel Le Bellac, « Introduction à l’information quantique », Hal open science, 2006.

   

  2-      2- David Deutsch et Richard Jozsa, « Rapid solutions of problems by quantum computation », Proceedings of the Royal Society of London A, vol. 439,‎ 1992. 

   

  3-      3- David Deutsch, « Quantum theory, the Church-Turing principle and the universal quantum computer », Proceedings of the Royal Society of London; Series A, Mathematical and Physical Sciences, vol. 400, n^o 1818,‎ juillet 1985.
• Select topic Forum

  Forum
  • Select activity Questions

    

    Questions Forum