Topic outline

  • About the Cours and the Author

    Collapse all Expand all

    University: Djilali Bounaama Khemis Miliana

    Faculty: Science of Matter and Computer Science

    Department: physics

    Speciality: theoretical physics

    Level: Master 1

    Module: Quantum Field Theory II

    Semester: 2

    Credit: 06

    Unit: Fundamental.

    Coefficient: 3. 

    Timetable: 1h30 min, 3 sessions per week (2 lectures and 1 TD)

    Teacher responsible for the course: Dr. FERMOUS Rachid.

    Grade: MCA 

     Assessment method: 

    The final assessment is carried out through:

    • Assessment of tutorials: which represents 50% (12 points for presentations, 5 points for attendance and 3 points for participation). 
    • A table-top final exam: which accounts for 50% of the final mark, and which covers everything you have seen in this course during the semester.
      To pass.

    • To pass the module, you must have an overall average of at least 10 out of 20.

       

  • Objectifs of the course

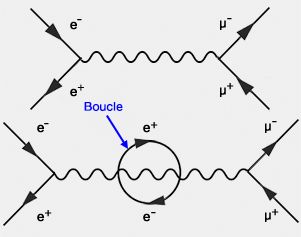
      The description of particle systems with relativistic energies where the particle-like (quantum) nature prevails over the wave-like (classical) nature.


  • Recommended prior knowledge

    Quantum Field Theory I

  • Course-Programm

    1    Lagrange formulation of quantum filed theory ....3

    1.1    Recall the formalism of Lagrange .  .  .  .  .  .  .  .  .  .  .3

    1.1.1     Principle of least action   .  .  .  .  .  .  .  .  .  .  3

    1.1.2     Euler-Lagrange equations     .  .  .  .  .  4

    1.1.3     Lagrangian choice   .  .  .  .  .  .  .  .  .  .  5

    1.1.4     Hamiltonian formulation   .  .  .  .  .  6

    1.2    Basic principle of quantum field theory  .  .  .  .  .  .  .  .  6

    1.2.1     Free scalar field     .  .  .  .  .  .  .  .  .  .  .  7

    1.2.2      Free complex scalar field  .  .  .  .  .  8

    1.2.3     Complex scalar field in the presence of an external electromagnetic field   .  .      8

    1.2.4     Remark .  .  .9

    2    Exercises 10

    3    Symmetries and conservation laws 11

    3.1    Example of transformation    .  .  .  .  .  .  .  .  .  11

    3.1.1     Space-time transformation    .  .  .  .  .  11

    3.1.2     Global phase.  .  .  .    12

    3.1.3     Local phase transformation.  .  .  .    12

    3.2    Noether’s theorem   .  .  .  .  .  .  .    12

    3.2.1     Statement   .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .    12

    3.2.2     Demonstration   .  .  .  .    13

    3.3    Energy-Momentum Tensor of the scalar field   .  .  18

    4    Exercises 20

    5    Dirac equation 21

    5.1    Dirac’s Hamiltonian   .  .  .  .  .  .  .  .  21

    5.2    The characteristics of Dirac matrices  .  .  .  .  .22

    5.3    Standard representation   .  .  .  .  .  .  .  .  25

    5.4    Free Dirac equation    .  .  .  .  .  .  .  .  .  26

    5.5    Physical interpretation of the negatives energies  .    28

    5.6    Current of free Dirac equation    .  .  .  .  .  .  .  .  .    29

    5.6.1     vector current and total charge     .  .  .  .  .  .  .  .    31

    5.7    Dirac equation in the presence of an external electromagnetic field  .  .  .  .  .    31

    5.8    Lagrangian of the complex spinor field   .  .  .  32

    5.9    Lagrangian of the complex spinor field in the presence of an external electromagnetic field.   .  .  .  .  .    33

    6    Exercises 35

    7    Somme References 40


  • First-Chapter


  • Exercises-First-Chapter

  • Second-Chapter


  • Exercises-Second-Chapter

  • Third-Chapter


  • Exercises-Third-Chapter


  • References

    1.    J.  P.  Derendinger,  Théorie  quantique  des  champs,  Presses  polytechnique  et  universitaires  
    romandes, 2001
    2.  S. Weinberg, Quantum theory of fields, 3 vols, Cambridge University Press, 1995,1996
    3.  J. J. Sakurai, Advanced quantum rnechanics, Addison-Wesley, 1967
    4.  J. D. Bjorken and S.D. Drell, Relativistic quantum fields, McGraw-Hill, 1965
    5.  F. Mandl et G.Shaw., Quantum field theory, Addison-Wesley, 1993
    6.  N. N. Bogoliubov, D. V. Shirkov, Introduction to the Theory of Quantized Fields (Interscience
    Monographs in Physics and Astronomy), John Wiley & Sons, 1959
    7.  R. Balian, du microscopique au macroscopique, vol. 2. École polytechnique, ellipses, 1982