Topic outline

  • Déscription du cours

    Collapse all Expand all

    Ce cours correspond au  programme de la matière Mathématiques II (Analyse 2 et Algèbre 2) enseigné  en première année, deuxième semestre aux étudiants la première année licence L.M.D de sciences de la matière (SM) et sciences et techniques (ST). Il offre un niveau de spécialisation élevé en Analyse et en Algèbre  tels le calcul différentiel et  intégral, la résolution d'équations différentielles, le développement limité et le calcul matriciel avec beaucoup d'applications très utiles pour le physicien ou le chimiste

     

  • Fiche de Contact

     

    Enseignant chargé de cours: Dr. Leila SLIMANE

    Grade: MCB      Spécialité: Mathématiques

    Contacts: l.slimane@univ-dbkm.dz

    Université: Djilali Bounaama Khemis Miliana

     Faculté: Science de la matière et l'informatique 

    Département: Physique   

    Niveau: L1 -Science de la matière - tronc commun

    Module: Mathématiques II  (Analyse II et Algèbre II)      Semestre: 2  

     Unité: Fondamentale      Crédit: 06            Coefficient: 3

    Horaire de cours : 1h30 min, 3 séance dans la semaine (2 cours et 1 TD) 

    Répartition du volume horaire semestriel : 45h cours  22h30 TD   Travail personnel :82h30

     Mode d'évaluation :  L'évaluation finale est réalisée à travers:

    •  Évaluation des travaux dirigés: qui représente 33% (12 points sur les intérrogation, 5 points sur la présence et 3 points sur la participation).
    • Un examen final sur table : qui compte pour 67% de la note finale, et qui porte sur tout ce qu’était enseigné de ce cours pendant le semestre.  

  • Prérequis

    L’étudiant doit être familiarisé avec les concepts et les notions présentés  dans le cours Mathématiques I tels que : définition d’une fonction réelles, les fonctions usuelles, limites, continuité, espaces vectoriels et les applications linéaire. Il doit maitriser les techniques utilisées  dans ce cours comme déterminer le  domaines de définition d’une fonction , calculer les limites, déterminer si une fonction et continue ou discontinue, de versifier si une application est linéaire ou non.


  • Objectifs du cours

     

    A la fin de ce cours, l’étudiant devrait être en mesure de:

    ·         Calculer les dérivées de différentes fonctions ainsi que leur développement limité.

    ·         Manipuler les opérations sur les matrices et le calcul des déterminants

    ·         Résoudre des systèmes d’équations linéaires par plusieurs méthodes.

    ·         Calculer  les intégrales des fonctions rationnelles, exponentielles, trigonométriques et polynomiales.

    ·         Manipuler les fonctions à plusieurs variables : Limite, continuité, dérivées partielles, intégrale double.

    ·           Résoudre des équations différentielles du premier et du second degré.

  • Topic 4

  • Plan du cours

     

    1.      Dérivées et Développement limités

    2.      Intégrales et primitives

    3.      Fonctions  à plusieurs Variables

    4.      Equations Différentielles 

    5.  Matrices, déterminants, Valeurs propres et Diagonalisation, Systèmes d'équations linéaires 


    l

  • Forum du cours de Mathématiques

    Chèrs étudiants , si vous des questions on peut les discutées ensemble ici. 

    Merci

  • Evaluation des acquis du cours Math1 (prérequis)

  • Chapitres1 et 2 : Dérivabilité et Développement Limités

    Ce chapitre est consacré aux dérivées : propriétés et règles de dérivation et aux développement limitées et leur applications.

     

  • Chapitre 3 :Intégrales et Primitives

     

    Ce chapitre traite le calcul des primitives et des intégrales ainsi que propriétés des intégrales définies et indéfines.  L'étudiant apprendra quelques techniques d'intégration : utiliser directement la table des primitives, changement de variables, intégration par partie, décomposition des fonctions rationnelles en des éléments simples,.

  • Chapitre 4 : Equations Différentielle

     

    Certains types  équations différentielles ordinaires (E.D.O)  d'ordre 1 er 2 sont présentés ainsi que leurs règles de résolution.

  • C hapitre 5 : Fonctions à Plusieurs Variables

     

    Les fonctions de plusieurs variables sont traitées dans cette partie. Les notions et les techniques de calcul de limites, continuité, dérivées partielles sont présentées dans ce cas. 

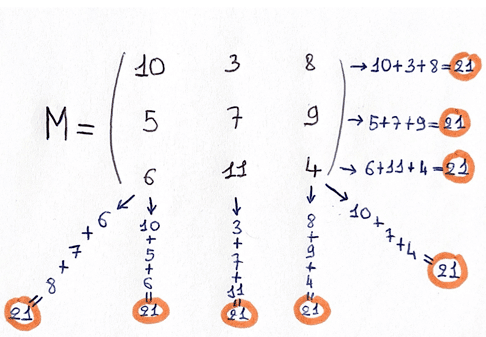
  • chapitres 6 et 7 : Matrices, Déterminants et Systèmes d'équations Linéaires

     

    Dans cette partie on présente la notion des matrices et des déterminants. L'étudiant sera capable à la fin de ce chapitre de manipuler des opérations sur les matrices (somme, produit, transposée,...),de calculer les déterminant en prenant en compte  leurs propriétés, les valeurs propres et les vecteur propres, faire la diagonalisation des matrices et  de résoudre des systèmes d'équations linéaires par des méthodes différentes.

  • Références

     

    1. Elie BELORIZKY, Outils mathématiques à l'usage des scientifiques et des ingénieurs, EDP Sciences, Paris, (2007).
    2. Walter APPEL, Mathématiques pour la physique et les physiciens!, 4ème Ed., H&K Edition, Paris, (2008).
    3. C. ASLANGUL, Des mathématiques pour les sciences, Concepts, méthodes et techniques pour la modélisation, De Boeck, Bruxelles (2011).
    4. C. ASLANGUL, Des mathématiques pour les sciences2, Corrigés détaillés et commentés des exercices et problèmes, De Boeck, Bruxelles (2013).
    5. Piskounov, Tome 2, Calcul différentiel et intégral, Ed. MIR, (1976).