Aperçu des sections

  • Fiche Contact

    Tout replier Tout déplier

    Université: Khemis-Miliana

    Département:  Mathematiques

    Niveau: M1 Analyse Mathématique et Applications

    Matière: Calcul fractionnaire

    Contenu de la matière :
    - Fonctions spéciales.
    • Définitions des fonctions Gamma et Beta.
    • Propriétés des fonctions Gamma et Beta.
    • Définition de la fonction de Mittag-Lefler.
    - Dérivées et Intégrales Fractionnaires.
    • Intégrales d’ordre arbitraire.
    • Dérivée d’ordre arbitraire.
    • Dérivée fractionnaire au sens de Grunwald-letnikov.
    • Dérivée fractionnaire au sens de Riemann-Liouville.
    • Dérivée fractionnaire au sens de Caputo.
    • Dérivée fractionnaire à gauche et à droite.
    - Opérations sur les dérivées fractionnaires.
    • Composition avec les dérivées entières.
    • Composition avec les dérivées fractionnaires.
    • Règle de Leibniz pour les dérivées fractionnaires

    Mode d’évaluation : Continu (40%), examen (60%).

  • Connaissances préalables recommandées

     1. Calcul différentiel,

    2. Théorie des EDO,

    3. Analyse fonctionnelle

  • Section 2

  • Les Objectives

    L'objectif de cette matière est de rappeler quelques notions élémentaires de calcul fractionnaire. Ces outils ont comme application (entre autres) l'existence et la non-existence des solutions pour certains types d’équations d’évolution.

  • Chapitre1: Fonctions spéciales

    Fonction gamma — Wikipédia

    Ce premier chapitre sera consacré aux éléments de base du calcul fractionnaire:

    1. Définition de la fonction Gamma

    2. Définition de la fonction bêta

    3. Définition de la fonction Mittag-Leffler

     

     

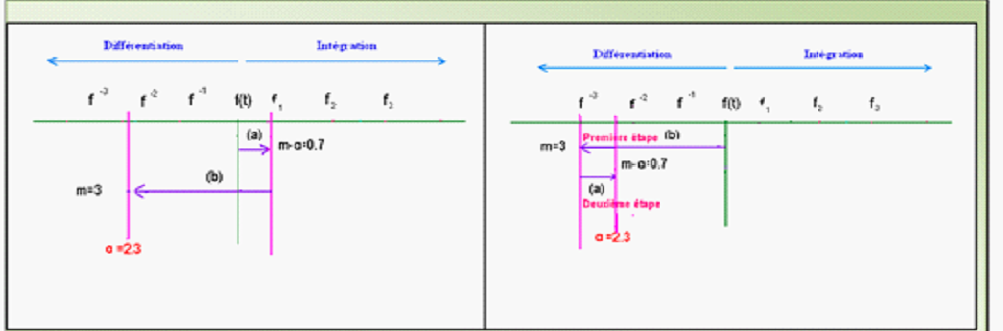
  • Chapitre2: Intégrales et dérivées fractionnaires

    L’objet du deuxième chapitre est l’étude des points suivants:

    1. Intégrales d’ordre arbitraire.
    2.  Dérivée d’ordre arbitraire.
    3.   Dérivée fractionnaire au sens de Grunwald-letnikov.
    4.  Dérivée fractionnaire au sens de Riemann-Liouville.
    5.  Dérivée fractionnaire au sens de Caputo.
    6.  Dérivée fractionnaire à gauche et à droite.

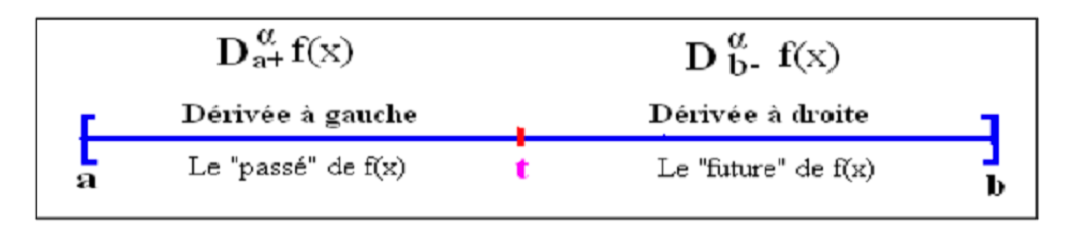
  • Capitre3: Opérations sur les dérivées fractionnaires

     

    Ce troisième chapitre portera sur les opérations sur les dérivées fractionnaires:

    1. Composition avec les dérivées entières.
    2.  Composition avec les dérivées fractionnaires.
    3.  Règle de Leibniz pour les dérivées fractionnaires.

  • References

    1. H. Dib, Equations différentielles fractionnaires, EDA-EDO (4ème Ecole) Tlemcen 23-27, mai 2009.
    2. A. A. Kilbas, H.M. Srivastava and J. J. Trujillo ; Theory and applications of fractional
      differential equations. Elsevier, Amsterdam, 2006.
    3. I. Podlubny ; “Fractional-order systems and fractional-order controllers,”UEF-03-94
      Slovak Academy of Science, Kosice, 1994.
    4. I. Podlubny ; Fractional differential equations. Academic Press, San Diego, 1999.
    5. G. Samko, A. A. Kilbas and O. I. Marichev ; Fractional integral and derivative, Theory
      and Applications, Gordon and Breach, Yverdon, 1993.