Séries et Équations Différentielles
Section outline
-
This document is the culmination of a decade's worth of dedicated teaching experience, spanning the years from 2013 to 2023, during which I had the privilege of instructing second-year undergraduate physics students. The content within these pages is a testament to the evolution and refinement of my teaching methods and materials over this substantial period.
Our primary focus lies in providing a comprehensive and meticulously crafted course curriculum that seamlessly integrates with the "Series and Differential Equations" course, an essential component of the Fundamental Teaching Unit (UEF-F121) tailored specifically for second-year license students pursuing degrees in fundamental physics. We intend that this material not only complements the established syllabus but enriches the learning experience, offering students a robust foundation in the subject matter.
-
University: Djilali Bounaama Khemis Miliana
Faculty: Science and Technology
Department: Material Sciences
Specialty: Fundamental physics
Level: License 2
Module: Series and differential equations
Semester: 03
Coefficient: 03
Lecturer: .
specialty: Physics
Diploma: Habilitation in theoretical physics.
Grade: MCA
Contact: You can contact me on mustapha.sadouki@univ-dbkm.dz
Assessment method: The final evaluation is carried out through a final exam.
To pass the module, the general average must be greater than or equal to 10 out of 20
-
The objectives of the course:
1. Comprehensive Understanding: The primary objective is to provide students with a comprehensive understanding of the mathematical concepts related to series and differential equations.
2. Seamless Integration: Ensure that the course curriculum seamlessly integrates with the "Series and Differential Equations" course, which is a crucial component of the Fundamental Teaching Unit (UEF-F121) tailored for second-year undergraduate physics students.
3. Enriched Learning Experience: Enhance the learning experience by offering a curriculum that not only complements the established syllabus but also enriches it, providing students with a robust foundation in the subject matter.
4. Versatility Across Disciplines: Recognize the potential applications of the material beyond fundamental physics. Aim to make the resource valuable for students pursuing undergraduate studies in various disciplines, including electronics, electromechanics, mechanical engineering, civil engineering, and automation.
5. Skill Development: Equip students with the necessary mathematical tools and problem-solving techniques required for a wide range of physics and engineering problems.
6. Demystification of Differential Equations: Break down and demystify differential equations, considering them a crucial language in science and engineering. Provide students with a clear understanding of their components and solving techniques.
7. Introduction to Series: Introduce students to the study of series, both numerical and integer, as a foundation for understanding infinite summations. This paves the way for a deeper exploration of Fourier series and their applications in diverse fields.
8. Exploration of Advanced Mathematical Tools: Explore advanced mathematical tools such as Fourier Transform and Laplace Transform, emphasizing their applications in signal processing, image analysis, quantum mechanics, and solving differential equations in engineering and physics.
Overall, the course aims to be a valuable resource that not only imparts theoretical knowledge but also fosters practical problem-solving skills, preparing students for success in the diverse and evolving fields of science and technology. -
Here are possible prerequisites that students might need before undertaking this course:
1. Calculus: A solid understanding of calculus, including concepts of differentiation and integration, is likely a fundamental prerequisite. This would ensure that students are familiar with the basic mathematical operations and concepts that will be built upon in the course.
2. Basic Physics Knowledge: Given that the course is designed for second-year undergraduate physics students, a foundational knowledge of basic physics principles and terminology may be assumed. This could include an understanding of classical mechanics, electromagnetism, and introductory quantum mechanics.
3. Mathematical Rigor: A comfort with mathematical rigor and formal proofs would be beneficial. Since the course involves solving differential equations, working with series, and exploring advanced mathematical tools, students should be prepared for a higher level of mathematical abstraction compared to introductory courses.
4. Algebra Skills: Proficiency in algebra is crucial for manipulating equations and understanding the relationships between variables. This includes solving equations, manipulating expressions, and understanding algebraic structures.
5. Linear Algebra: Some familiarity with linear algebra might be helpful, especially when dealing with concepts like Fourier series and transforms. Understanding matrices, vectors, and basic linear algebra operations could be relevant.
-

We delve into the world of integrals, exploring both their basic and more complex forms, equipping students with the mathematical tools needed for a wide range of physics and engineering problems.
-

This chapter guides students through the subtleties of improper integrals, demonstrating their significance in various real-world scenarios.
-
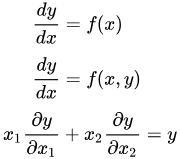
We demystify differential equations, a crucial language of science, and engineering, breaking them down into understandable components and solving techniques.
-

The study of series, both numerical and integer, introduces students to the realm of infinite summations, paving the way for a deeper understanding of Fourier series and their applications in diverse fields.
-

This chapter explores the Fourier transform, a powerful mathematical tool that finds applications in signal processing, image analysis, and quantum mechanics, among others.
-
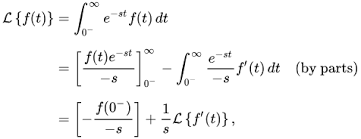
We conclude with a thorough examination of the Laplace transform, a transformative technique essential for solving differential equations, making it indispensable in engineering and physics.
-
Bibliography
[1] Appel, W. (2008). Mathématiques pour la physique et les physiciens (4th ed.). H&K Edition.
[2] Belorizky, E. (2007). Outils mathématiques à l'usage des scientifiques et des ingénieurs. EDP Sciences.
[3] Aslangul, C. (2011). Des mathématiques pour les sciences: Concepts, méthodes et techniques pour la modélisation. De Boeck.
[4] Nicaise, S. (2000). Analyse numérique et équations aux dérivées partielles: cours et problèmes résolus. Dunod.
[5] Tritiak, A. (1981). Cours équations différentielles ordinaires. Université de Constantine Algérie.
[6] Nadir, M. (2004). Cours équations différentielles ordinaires. Université de Msila Algérie.
[7] Krasnov, M., Kisselev, A., & Makarenko, G. (1978). Recueil de problèmes sur les équations différentielles ordinaires. Editions Mir.
[8] Meyer, X. (2005). Equations aux dérivées partielles: Cours et exercices corrigés. INPT-ENSIACET, Toulouse, France.
[9] Bekka, B. (2014). Suites et séries de fonctions. Cours L3 Rennes.

