informatique 1
Topic outline
-
Chapitre1:
Introduction à l’informatique
1. Introduction
L’informatique est une «science» qui permet de traiter l’information de façon automatique.
L’ordinateur est un appareil très puissant permettant de traiter les informations avec une très grande vitesse, un degré de précision élevée et permet de stocker toutes ces informations.
1-1 La partie matérielle
C’est la partie physique du système informatique.
Elle est divisée en deux parties:
a) L’unité centrale
b) Les périphériques
a) L’unité centrale
Où s’effectue l’essentiel du traitement de l’information.
Sur la carte mère, on trouve
Le processeur: C’est l’unité d’exécution, Il effectue les opérations arithmétiques et logiques.
La mémoire: C’est l’unité de stockage, elle sauvegarde les informations. On distingue la mémoire interne et la mémoire externe.
La mémoire interne: elle est appelée disque dur sans elle la machine ne peut fonctionner.
La mémoire externe: C’est celle qui est déplaçable. Exemple : les disquettes, le CD ROM, le DVD ROM, le disque zip, la clé USB. Les périphériques
b)Les périphériques:
Ce sont les accessoires que l’on peut connecter à l’ordinateur. On distingue les périphériques d’entrée et les périphériques de sortie.
Les périphériques d’entrée: ils permettent de véhiculer les informations du monde extérieur vers la mémoire de l’ordinateur. (Le clavier, la souris et le scanner)
Les périphériques de sortie: ils permettent de véhiculer les informations de la mémoire de l’ordinateur vers le monde extérieur. L’écran, l’imprimante, les haut-parleurs, etc.
1-2 La partie logicielle:
Il est important de savoir qu’un logiciel est un programme. On distingue deux types:
Le système d’exploitation: Windows7 (Microsoft), Léopard (MacosX)
Le logiciel d’application: Microsoft Office, Open Office, etc
-
-
Chapitre II CODAGE BINAIRE
I. Introduction
Le traitement de l’information (Image, mot, nombre,…etc.) est effectué par l’ordinateur ou calculateur électronique. Les circuits électroniques qui les constituent ne peuvent prendre que deux états représentés par 0 et 1. Donc, le langage utilisé dans ces machines est appelé système de numération binaire (suite de 0 et de 1).
II. Différents systèmes de numération
Il existe quatre systèmes de numération qui sont :
- Système décimal ;
- Système binaire ;
- Système octal ;
- Système hexadécimal.
Système décimal
C’est un système utilisé dans le monde extérieur, les chiffres utilisés sont des entiers composés par des valeurs de 0 à 9. La base de ce système est 10.
Exemple
1995 : ce nombre s’écrit dans le système à base 10 sous la forme :
1* 103 + 9 * 102 + 9 * 101 + 5 * 10°
Système binaire
C’est le système qui est utilisé par la machine (l’ordinateur), il est composé seulement par des suites binaires (1 et 0). La base de ce système est 2.
Exemple
1001101 : la valeur décimale de cette suite est :
1* 2 6 + 0 * 25 + 0 * 24 + 1* 23 + 1* 22 + 0 * 2' +1*2° =77
Chaque chiffre binaire (0 ou 1) est appelé bit qu’on note par b, et toutes combinaisons binaires composées de huit bits est appelée Octet.
Example: 11100100
B0 = 0, b1= 0, b2=l, b3= 0, b4=0, b5= 1, b6=l ,b7= 1
Seize (16) bits est appelée « mot-mémoire » ou bien mot machine
Example: 1110001010100110
B0 = 0 b1= 1 b2 = 1 b3 = 0 b4= 0 b5= 1 b14=l b15= l
Système octal
Le système décimal est celui qui est le plus utilisé par l’homme, et le système binaire est celui le plus utilisé dans les ordinateurs.
Le système binaire présente l’inconvénient d’être difficile à manipuler par l’homme car les nombres sont représentés par une suite de 0 et 1 qu’il est difficile de lire ou d’interpréter sans erreur. Il est donc plus commode d’écrire les nombres codés en binaire sous une forme plus compacte, dans un système dont la base est une puissance de 2, de façon à permettre une conversion facile avec le système binaire.
Nous définissons dans ce paragraphe le système octal, et plus loin le système hexadécimal.
Certains calculateurs numériques utilisent le système octal qui est un système de numération dont la base 8.
On dispose de huit symboles pour représenter un nombre dans le système octal. Ce sont les chiffres successifs allant de 0 à 7. Chaque chiffre d’un nombre octal a une pondération égale à la valeur du chiffre multipliée par la puissance de 8 correspondants au rang qu’il occupe dans le nombre.
Exemple : N = 5368
- Chiffre 5 3 6
- Puissance 82 81 80
- Pondération 320 24 6
L’addition des pondérations donne l’équivalent décimal du nombre octal considéré.
320+24+6 = 350
Soit 5368 ⇒ 35010
Système hexadécimal
Ce système est utilisé sur la plupart des nouveaux calculateurs numériques. Sa base est égale à 16. On dispose de 16 symboles pour représenter un nombre hexadécimal. Ces symboles sont les 10 digits du système décimal auxquels on a ajouté les 6 premières lettres de l’alphabet. Les 16 symboles sont alors :
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Chaque signe d’un nombre hexadécimal a une pondération qui s’obtient en multiplient la valeur numérique du symbole par la puissance de 16 correspondant au rang qu’il occupe dans le nombre.
Exemple : N = 4CA216
- Signes
4
C
A
2
- Puissance
163
162
161
160
- Pondérations
16384
3072
160
2
L’addition des pondérations donne l’équivalent décimal du nombre hexadécimal considéré :
16384+3072+160+2 = 19618
Soit 4AC216 ⇒ 1961810
L’intérêt de ces deux systèmes vient de ce que 8 et 16 ont des puissances entières de groupe de 3 et 4 bits et par conséquent, on peut effectuer les conversions Octale / Décimale ainsi que Hexadécimale / Décimale. (Voir Tableau):
Nombre
décimal
Binaire
octal
Hexadécimal
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
10001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
19
10011
23
13
20
10100
24
14
III. Transformations (conversions)
Décimal / Binaire ,
Pour convertir un nombre décimal en un nombre binaire, diviser continûment le nombre décimal par la valeur 2, retenir la suite des restes de chaque division en commençant de bas en haut pour avoir le nombre équivalent.
33
2
1
16
2
0
8
2
0
4
2
0
2
2
0
1
1
Exemple :
(33)10 = (100001)2
Dans le cas où le nombre donné dispose d’une partie fractionnaire, l’opération de conversion se fait de la manière suivante :
· Multiplier la partie, fractionnaire du nombre donné par 2 et retenir la partie entière du résultat trouvé.
· Continuer à multiplier successivement par la valeur 2 les parties fractionnaires obtenues pendant chaque opération tout en retenant leurs parties entières, jusqu'à ce qu’on obtienne une partie fractionnaire nulle ou déjà obtenue, sinon ce sera une suite binaire infinie et dans ce cas , on peut se limiter à quelques bits (problème d’arrondi).
· Le résultat de cette conversion est l'ensemble, des parties entières conservées à chaque étape de multiplication.
Exemple :
Transformer le numéro 23 en binaire ? (23)10 = (10111)2
Exemple :
Convertir le nombre (23.625) de la base 10 à la base 2.
La partie entière 23 est déjà déterminée, son résultat est : (23)10 = (1011l) 2. Pour la partie fractionnaire 0.625, on procède comme suit :
0.625 * 2 = 1.250
0.250 * 2 = 0.500
0.500 * 2 = 1.00
On constate que la dernière partie fractionnaire est nulle, donc le résultat sera :
(0.625)10 = (0.101)2
Le résultat final : (23.625)10 = (10111.101 )2 Prenons le cas infini par exemple (23.56)10
Pour (23)10 c'est toujours (10111): mais pour la partie fractionnaire (0.56)10, on aura :
0.56 *2=1.12
0.12 *2 = 0.24
0.24*2 = 0.48
0.48 * 2 = 0.96
0.96*2 = 1.92
0.92 * 2= 1.84 etc.,
On remarque, si on continue l'opération de multiplication de la partie fractionnaire par la valeur 2 , on ne tombe jamais sur le critère d’arrêt de cette opération , cela veut dire que la suite binaire est infinie et nous pouvons la tronquer en nous limitant à un certain nombre de bits .
D’où le résultat final de : (23.56)10 est (10111.100011)2
III.2. binaire/décimale
Pour convertir une suite binaire en système décimal, on procède de la manière suivante
Faisons l’addition de tous les termes de la forme (bit * 2), en commençant de droite à gauche pour les parties entières et de gauche à droite pour les parties fractionnaires.
« bit » : peut prendre les valeurs 0 ou 1. Le symbole " i ” indique les puissances de 2 qui sont positives pour les parties entières et vont de 0 à (n-1) et négatives pour les parties fractionnaires et vont de la valeur (-1) jusqu’à (-m) avec n et m sont respectivement les longueurs de la suite binaire avant et après la virgule.
Exemple :
(10110 )2 =0*2°+ 1 * 21 + 1 * 22 + 0 *23 + 1 * 24 = (22)10
(10110 . 1011)2 = ?
- Pour la partie entière (10110)2 = (22)10
- Pour la partie fractionnaire : (0.1011)2= (1*2-1 + 0*2-2 + 1 *2-3 + 1* 2-4 )
Le résultat final :
(10110.1011)2 = (22.6875)10
III.3 Binaire /Octale - Binaire / Hexadécimale
La conversion d’une suite binaire en système octal et en système hexadécimal, se fait respectivement par le regroupement de trois et de quatre bits, en commençant de droite à gauche, chaque-bloc de bits sera convertible en système demandé
Exemple :
(1010110111)2 = (?)8 et (?)16
En base 8 (regroupement par des blocs de trois bits):
(111)2 = 7 ; (110)2 = 6 ; (010)2=2 ; (001 )2 = 1 D'où (101011011l)2 = (1267)8
- En base 16 (regroupement par des blocs de quatre bits), |
(0111)2 = 7 ; (1011)2 = B ; (0010)2 = 2 D'où (1010110111); = (2B7)16
Opérations arithmétiques et logiques
Addition en binaire
L'addition est réalisée bit à bit.1 +0 = 1
1 +1 = 10
1 +1 + 1 = 11
Produit logique en binaire
La fonction ET est appliquée bit à bit
Les nombres signés
En binaire, le négatif d'un nombre est son complément à 2, c'est-à-dire son complément+1.
Soient deux nombres A=104 et B=42. A- B =A+ (- B)
-
-
Chapitre 3: Algorithme et Programmation
Introduction :
· Les étapes pour la résolution d’un Problème (Mathématique) sont :
a)Analyse du problème.
b) Etablir l’algorithmique.
c) Programmation (utilisation d’un langage de programmation).
d) Vérification et correction du programme.
e) Exécution du programme.
I. Notions d’Algorithme:
Le mot algorithme vient du nom du célèbre mathématicien arabe Al Khawarizmi (ABU JA'FAR MOHAMMED BEN MUSSA AL-KHWARISMI) origine de l’ancienne ville de KHAWARISM.
Un algorithme est le résultat de la décomposition d’un problème complexe en opérations élémentaires à exécuter en plusieurs étapes successives. En d’autre terme, un algorithme est une suite de règles, de raisonnements ou d’opérations, qui transforment des grandeurs données (données d’entrée) en d’autres grandeurs (données de sortie).
· Structure Générale d’un Algorithme
Parties principale
a. L’entête : qui contient le nom de l’algorithme permettant de l’identifier.
b. Les déclarations de constantes, variables, structure
………….. : cette partie de l’algorithme permet de déclarer tout type de variable, constante ou structure.
c. Les déclarations de fonctions et procédures …………. :
dans cette partie toutes les fonctions et les sous programmes du problème sont déclarées.;
d. Corps de l’algorithmique …………………………. :
cette partie de l’algorithme contient toutes les instructions permettant de traiter et de résoudre le problème posé.
début de l’algorithme
instruction1; instruction2; instruction3;
fin de l’algorithme
Exemple :
Algorithme nom d’algorithme
Declaration des constantes
Declaration des variables
Début
Instruction 1
Instruction 2
----------------
----------------
----------------
-----------------
Instruction n
Fin nom d’algorithme
· Notions d’Organigramme
Un organigramme est une représentation graphique d’un algorithme, il permet de schématiser graphiquement la solution d’un problème. Un organigramme permet de mieux visualiser la démarche de résolution d’un problème, il est construit à partir d un formalisme comprenant cinq simples symboles normalisés qui sont reliés entre eux par des lignes de liaisons, ces symboles sont :
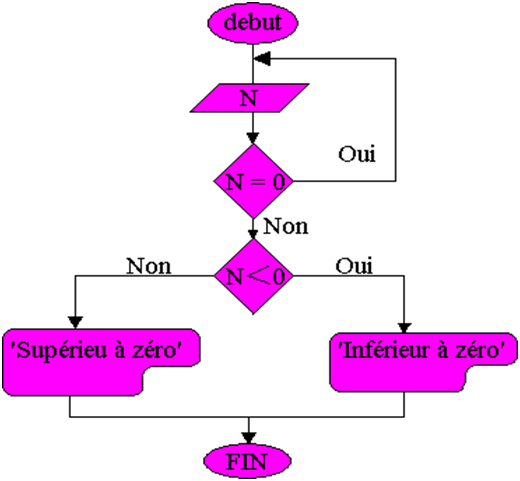
Exemple : Ecrire un organigramme qui lit un nombre N non nul et affiche le message: inférieure à "0" ou supérieur à "0" suivant sa valeur.
