TP Méthodes Numériques (M)

Aperçu des sections

• Sélectionner la section thématique Fiche de contact بطاقة تعريفية للمادة

  Fiche de contact بطاقة تعريفية للمادة

  Tout replier Tout déplier

  Matière : TP Méthodes Numériques

  Unité d'Enseignement Méthodologique : (UEM)

  Niveau : L2 Génie Civil

  Volume Horaire : 22.5 h (TP : 1h30m/semaine)

  Crédit = 2

  Coefficient : 1

  Enseignant : Dr. Abdellah BOUDINA

  E-Mail : a.boudina@univ-dbkm.dz

   

  • Sélectionner l'activité Announcements

    

    Announcements Forum
• Sélectionner la section thématique L'objectifs أهداف التعليم

  L'objectifs أهداف التعليم

  • Les objectifs d'un travaux pratiques (TP) en méthodes numériques sont généralement axés sur l'application des concepts théoriques appris en classe à des problèmes concrets. Voici quelques objectifs typiques d'un TP en méthodes numériques :

    1. Compréhension pratique des algorithmes: Les TP permettent aux étudiants de mettre en pratique les algorithmes et les méthodes numériques discutés en classe. 

    2. Maîtrise des outils de programmation: Les TP fournissent souvent l'occasion aux étudiants de développer leurs compétences en programmation en mettant en œuvre les méthodes numériques à l'aide de langages comme MATLAB.

    3. Validation des résultats: Les étudiants apprennent à évaluer la validité de leurs résultats numériques en comparant les solutions obtenues avec des résultats analytiques si est possible.

    4. Analyse des performances: Les TP permettent aux étudiants d'évaluer les performances des algorithmes en termes de temps de calcul, de précision et de stabilité.

    5. Application à des problèmes réels: Les TP peuvent impliquer la résolution de problèmes réels provenant de domaines tels que la physique, l'ingénierie, les sciences de la vie, etc. Cela montre aux étudiants comment les méthodes numériques peuvent être utilisées pour résoudre des problèmes du monde réel.

    6. Travail en équipe et communication: Dans certains cas, les TP peuvent être réalisés en équipe, ce qui permet aux étudiants de développer leurs compétences en travail d'équipe et en communication en collaborant avec leurs pairs pour résoudre les problèmes proposés.

    En résumé, les TP en méthodes numériques visent à compléter l'apprentissage théorique en fournissant aux étudiants une expérience pratique de l'application des techniques numériques à des problèmes réels, tout en développant leurs compétences en programmation, en analyse et en résolution de problèmes.

      
• Sélectionner la section thématique Pré-requis

  Pré-requis

  Connaissances préalables recommandées: 

  • Algebre linéaire
  • Méthode numérique
  • Informatique 2
  • Informatique 3
• Sélectionner la section thématique Modalités d’évaluation

  Modalités d’évaluation

  Mode d’évaluation : 

  Contrôle continu : 100 %.
• Sélectionner la section thématique الخريطة الذهنية

  الخريطة الذهنية

  
• Sélectionner la section thématique Contenu de la matière

  Contenu de la matière

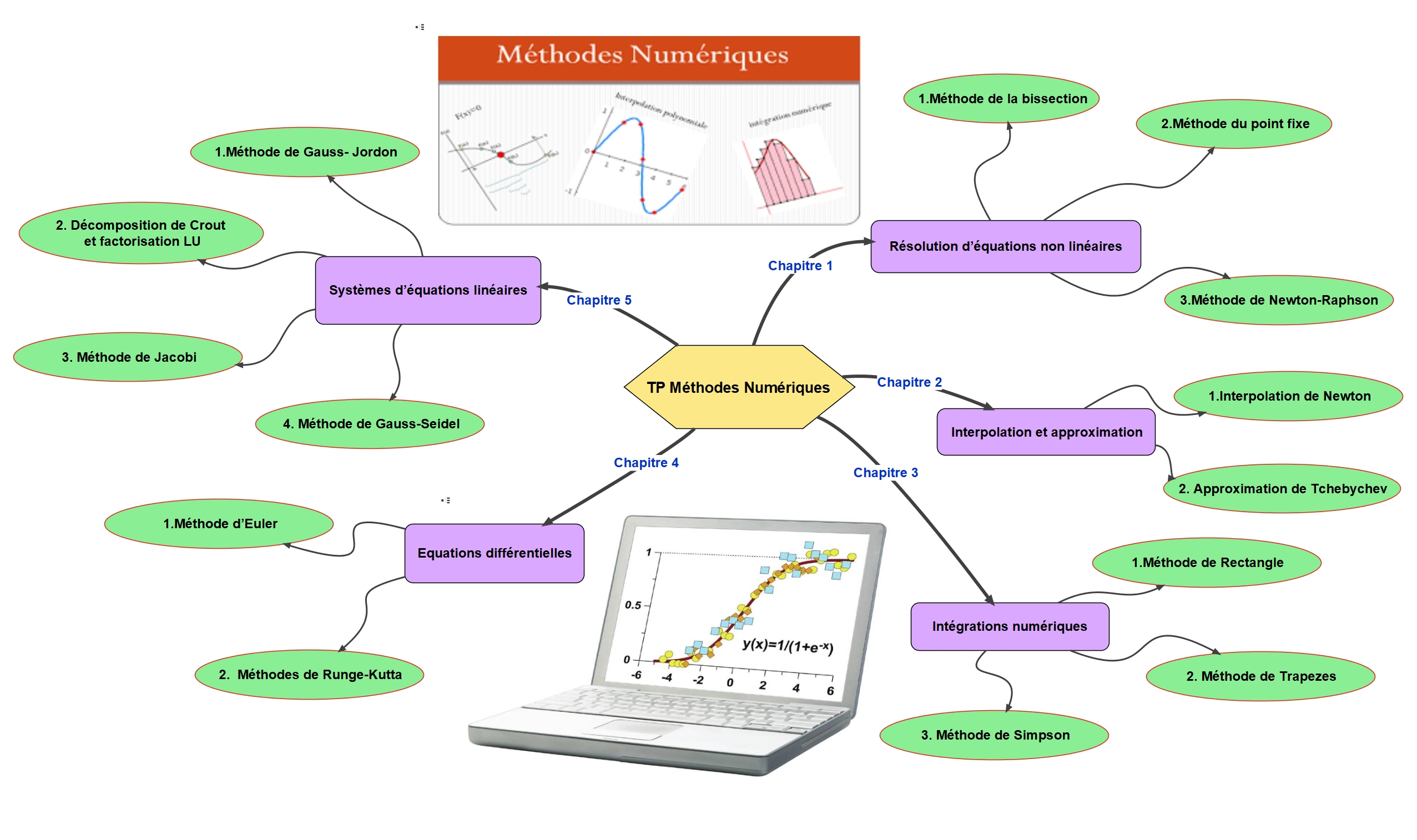
  Chapitre 1 : Résolution d’équations non linéaires

  • 1.Méthode de la bissection.
  • 2. Méthode des points fixes,
  • 3. Méthode de Newton-Raphson

  Chapitre 2 : Interpolation et approximation 

  • 1.Interpolation de Newton,
  • 2. Approximation de Tchebychev

  Chapitre 3 : Intégrations numériques

  • 1.Méthode de Rectangle,
  • 2. Méthode de Trapezes,
  • 3. Méthode de Simpson

  Chapitre 4 : Equations différentielles

  • 1.Méthode d’Euler,
  • 2.  Méthodes de Runge-Kutta

  Chapitre 5 : Systèmes d’équations linéaires

  • 1.Méthode de Gauss- Jordon,
  • 2. Décomposition de Crout et factorisation LU,
  • 3. Méthode de Jacobi, 4. Méthode de Gauss-Seidel
• Sélectionner la section thématique TP 01 Résolution des équations non linéaires

  TP 01 Résolution des équations non linéaires
  • Sélectionner l'activité 1- Méthode de bissection

    

    1- Méthode de bissection Leçon
  • Sélectionner l'activité 2- Méthode de point fixe

    

    2- Méthode de point fixe Leçon
  • Sélectionner l'activité 3- Méthode de Newton

    

    3- Méthode de Newton Leçon
  • Sélectionner l'activité Exemple 01 Méthode de bissection

    Exemple 01

  • Sélectionner l'activité Exemple 2 : Méthode de point fixe

    Exemple 2 :

  • Sélectionner l'activité Exemple 3 Méthode de Newton-Raphson

    Exemple 3

• Sélectionner la section thématique TP02

  TP02

  Exemple 1

   

  Exemple 2
• Sélectionner la section thématique TP03

  TP03

  Exemple 1

   

  Exemple 2
• Sélectionner la section thématique TP04

  TP04

  Exemple 1

   

  Exemple 2
• Sélectionner la section thématique TP 05

  TP 05

  Exemple 1
• Sélectionner la section thématique Activités

  Activités

  Tout rapport (compte-rendu) doit être organisé comme suit:

  1- Page de garde (Nom, Prénom, Groupe, TP, .... )

  2- Une introduction à la méthode étudiée.

  3- La partie théorique est manuscrite (بخط اليد)

  4- La partie pratique contient le programme de calcul avec l'exemple et les résultats

  5- Conclusion avec comparaison.

  6- Références
• Sélectionner la section thématique Test

  Test
• Sélectionner la section thématique Bibliographie

  Bibliographie

  1.      Algorithmique et calcul numérique : travaux pratiques résolus et programmation avec les logiciels Scilab et Python / José Ouin,  . - Paris : Ellipses, 2013 . - 189 p.

  2.      Mathématiques avec Scilab : guide de calcul programmation représentations graphiques ; conforme au nouveau programme MPSI / Bouchaib Radi, ; Abdelkhalak El Hami . - Paris : Ellipses, 2015 . - 180 p.

  3.      Méthodes numériques appliquées : pour le scientifique et l'ingénieur / Jean-Philippe Grivet,  - Paris : EDP sciences, 2009 . - 371 p.