Fourth axis: determinant and inverse of the matrix.

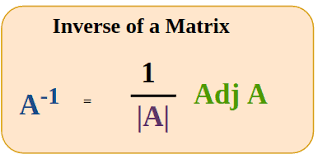
Matrices have been used for a long time in solving linear equations, and are the oldest form to use

Matrices in Solving Equations is a Chinese text called “The Nine Chapters on the Art of Mathematics,” which was written around the third century B.C. It also includes a study of the principle of determinants.

The inverse matrix of a matrix A is denoted by A−1. The inverse of matrix A is the process of searching for matrix B referred to above. A matrix is invertible if and only if its determinant differs from zero. Thus, it is irreversible if and only if its determinant equals zero.

Upon completion of this axis, the student will be familiar with the objectives of the axis based on Bloom’s levels of knowledge:

1. Knowledge and memory level: Students at this level retrieve and organize information from memory (prior acquisitions), where students learn about the determinants and inverses of a matrix, and provide them with the necessary skills that enable them to find the inverses of a matrix. The student is given multiple choice questions, and is asked to answer them. They can also be given fill-in-the-blank questions, the goal of which is to restore his tribal gains related to the axis.

2. The level of comprehension and comprehension: The student identifies and identifies the various variables and concepts related to the fourth axis. Here we give the student some various questions based on what was learned and evaluated for the lesson.

3. Application level: The student is able to perform operations on the determinants and inverses of matrices and learn about various methods for doing so.

4. Level of analysis: The student distinguishes the various operations related to the axis.

5. Structure level: Students organize information in different ways through brainstorming.

6. Evaluation level: The student evaluates and evaluates all the information acquired so that decisions are made based on the specified criteria. We develop a final exercise in which he identifies the various operations of determinants and inverses of the matrix.